Suggestion for using this website

Many beginner guitar players start out by memorizing common chord shapes. While this is a perfectly valid method to learn the guitar, it isn't the most efficient way because they are not understanding how the chord is constructed in the first place.

Common question that beginners ask are:

  • How many chords are there?
  • Do we really need to memorize all of them?
  • Do we need to memorize the notes on the fretboard?

    • Theoretically, we can create over 2000 chord shapes on the guitar fretboard, and let's be realistic, no one memorizes all of them. What I want to emphasize is that there is absolutely no need to memorize chords once you understand how different chord types are formed in terms of formulas written above, and understanding the interval relationship on the fretboard to spot out the thirds, fifths, seventh, etc... relative to the target root note.

    Instead of memorizing the notes on the fretboard from scratch, try to see the fretboard purely in terms of intervals from any root note. This is extremely useful for quick chord construction.

    So my suggestion for using this website is to:

  • Read over the basic guitar theory section, understanding the chord formulas
  • Go to the interval generator and experiment the interval relationship of the fretboard until you feel comfortable with it
  • Finally, go to the chord generator tool and play around forming different chords with different roots, adding extensions, and so on

    • Internalising the concepts of the theory behind chord construction for each chord type, learning where the intervals are located on the fretboard, and understanding the concept of guide tones, you will be able to construct any chord type you will ever need. This website aims to help users achieve this goal by providing visual and hands-on application to have on their side as they are learning these concepts.

    Terminologies

    A chord is any group of three or more notes played together, usually stacked on top of each other from a particular scale.

    A scale is a sequence of notes divided using intervals in order.

    A major scale has the formula 1 2 3 4 5 6 7 and is the basis of describing all other scales (ie. if you flatten or sharpen any note in that formula, it becomes a different, distinctive scale).

    These numbers (first, third, fifth, or 1 3 5) are called intervals and it defines the distance in pitch between two notes on a scale.

    Major chord

    For example, the C Major scale has is composed of C D E F G A B C

    When you take the first, third and fifth notes (C, E and G) and play them together, it becomes a C Major chord: (C) D (E) F (G) A B C.

    The first, third, and fifth notes of a major scale form a major chord. This is true for any major scale (ie. in any key), and is given by the formula 1 3 5.

    A set of three notes played together is called a triad. The C major chord is a triad of C E and G.

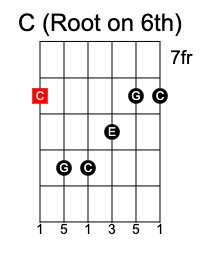
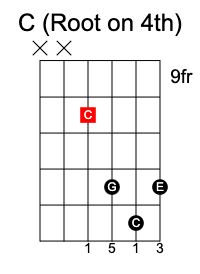
    Minor chord

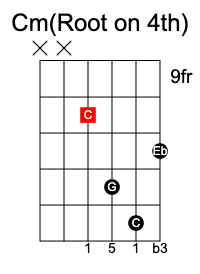
    If we flatten the third from the formula above to generate 1 b3 5, it becomes a minor chord.

    Using C as the root note, a C minor chord consists of the notes C Eb G.

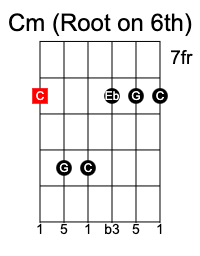
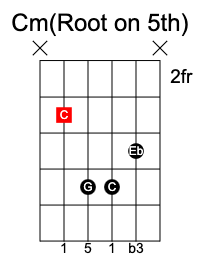
    Diminished chord

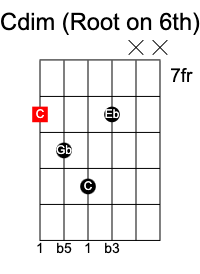
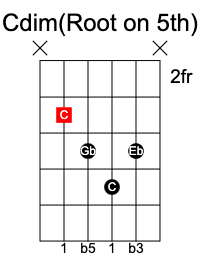
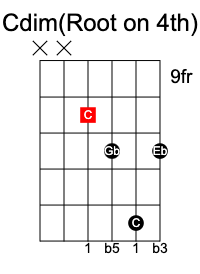
    If we flatten both the third and fifth notes from a major chord, it becomes a diminished chord. It has the formula 1 b3 b5.

    A C dim chord consists of C Eb Gb.

    Augmented chord

    An augmented chord has the formula 1 3 #5.

    A C aug chord consists of C E G#.

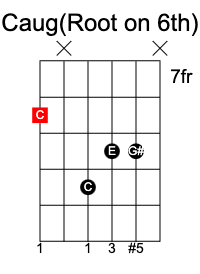
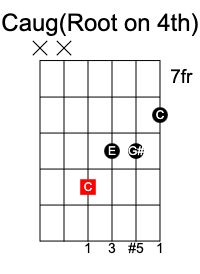
    Suspended chords

    These are chords that do not include a 3rd.

    In a sus2 chord, the 3rd is replaced with the 2nd of the scale, and results in the formula 1 2 5.

    C sus2 chord has the notes C D G.

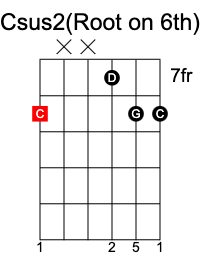
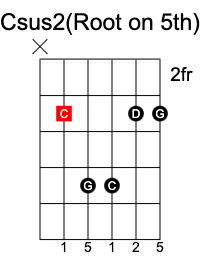
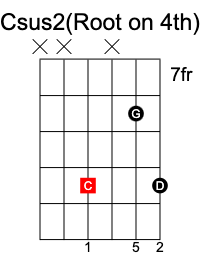
    In a sus4 chord, the 3rd is replaced with the 4th of the scale, and results in the formula 1 4 5.

    C sus4 chord has the notes C F G.

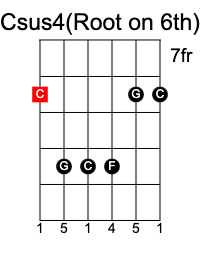
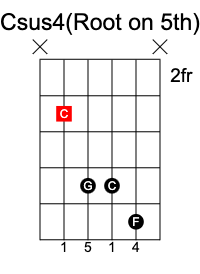
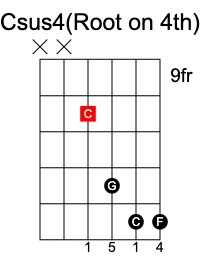
    Major 7th chord

    To create a major 7th chord, we extend the major chord formula 1 3 5 by adding an extra 7 at the end to create 1 3 5 7.

    C Maj7 chord has the notes C E G B.

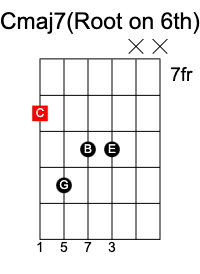
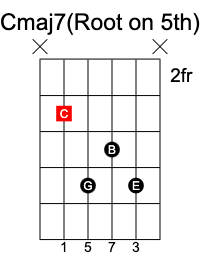
    Minor 7th chord

    A minor 7 chord is formed by extending the minor triad by adding a b7 at the end to create the formula 1 b3 5 b7.

    C minor7 chord has the notes C Eb G Bb.

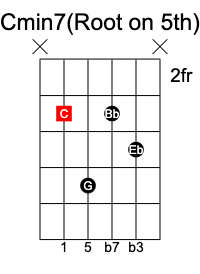
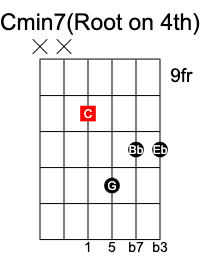
    Minor 7 flat 5 chord

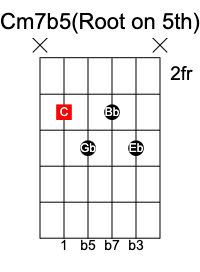
    A (diminished) minor b5 chord with an added b7 is called a minor 7 flat 5, or m7b5 chord. It has the formula 1 b3 b5 b7.

    C m7b5 chord has the notes C Eb Gb Bb.

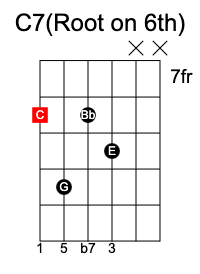
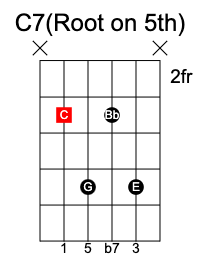
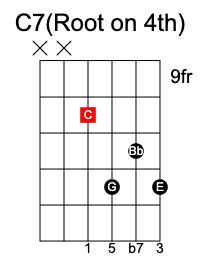
    Dominant 7th chord

    It is formed by adding a b7 to a major triad 1 3 5 to form 1 3 5 b7.

    C7 chord has the notes C E G Bb.

    Summary

    Chord Type Construction Notes often omitted
    Maj 1 3 5
    Min 1 b3 5
    Dim (mb5) 1 b3 b5
    Aug (Maj#5) 1 3 #5
    Maj7 1 3 5 7
    Min7 1 b3 5 b7
    7 1 3 5 b7
    m7b5 1 b3 b5 b7
    Dim7 1 b3 b5 bb7
    m(Maj7) 1 b3 5 7
    m(Maj9) 1 b3 5 7 9 5
    Maj9 1 3 5 7 9 5
    m9 1 b3 5 7 9 5
    9 1 3 5 b7 9 5
    m7b9b5 1 b3 b5 b7 b9 1
    m9b5 1 b3 b5 b7 9 1
    Maj11 1 3 5 7 9 11 3 9
    Maj7sus4 1 5 7 11
    m11 1 b3 5 b7 9 11 1 5 9
    11 1 3 5 b7 9 11 1 5 9
    m11b9b5 1 b3 b5 b7 b9 11 1 b5 b9
    Maj13 1 3 5 7 9 11 13 1 9 11
    Maj13sus4 1 4 5 7 9 11 13 1 5 9 11
    m13 1 b3 5 b7 9 11 13 1 5 9 11
    13 1 3 5 b7 9 11 13 1 11
    7 alt 1 3 5 b7 + any of b9, #9, b5(#11), #5(b13) 1 5

    Further readings

    Instead of simply listing chord diagragms, this book teaches readers how to construct guitar chords from scratch using interval relationships on the fretboard.

    Highly recommended for both beginners and intermediate players if you are looking to learn and apply chord theories in a greater depth.